원기둥이란?
원기둥은 위아래에 합동인 두 원이 평행하고 이를 감싸는 옆면이 둘러싸는 입체도형입니다. 이 원기둥을 펼치면 어떤 모양이 되는지를 살펴봅시다.
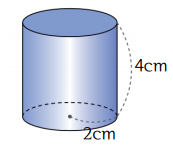
예) 위 도형은 반지름이 2cm인 두 원이 밑면으로 평행하고, 높이가 4cm인 원기둥입니다.
원기둥의 다른 예로는 다음과 같습니다.
이때 원기둥을 갈라 펼친 도형을 원기둥의 전개도라고 합니다.
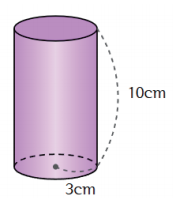
반지름이 3cm, 높이가 10cm인 원기둥을 잘라 펼치면 다음과 같습니다. (단, 원주율을 3으로 놓음)
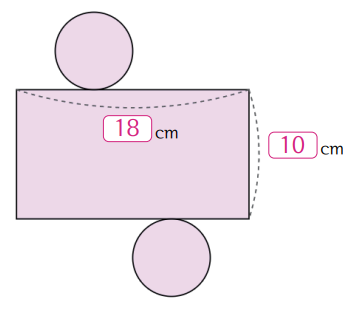
원기둥의 전개도는 크게 세 부분으로 구성됩니다. 첫 번째는 위쪽의 원, 두 번째는 아래쪽의 원, 그리고 세 번째는 원기둥을 감싸는 옆면을 펼친 직사각형입니다. 이때 두 원은 밑면이 됩니다.
옆면을 가위로 밑면에 수직하도록 자르면, 둥근 면이 펼쳐지면서 직사각형 모양이 됩니다. 이때 직사각형의 세로 길이는 원기둥의 높이와 같고, 가로 길이는 밑면인 원의 둘레에 해당합니다. 즉, 가로 길이는 원의 둘레인 지름 × 3.14 또는 2 × 반지름 × 3.14가 됩니다.
[참고] 원주율은 3, 3.1, 3.14중에 하나로 물어봅니다. 문제에서 원주율을 얼마로 약속했는지 파악해야 합니다.
원기둥의 전개도 분석하기
예) 반지름 6cm, 높이 8cm인 원기둥의 전개도를 생각해 봅시다.
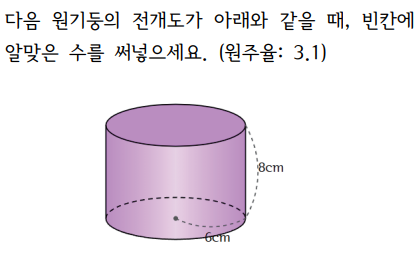
위아래 원의 모양은 반지름 6cm인 원 두 개입니다.
옆면 직사각형은 가로 길이가 원의 둘레인 12 × 3.1 = 37.2cm, 세로가 높이인 8cm입니다.
즉, 전개도는 반지름 3cm인 원 두 개와 가로 37.2cm, 세로 8cm인 직사각형으로 이루어집니다.
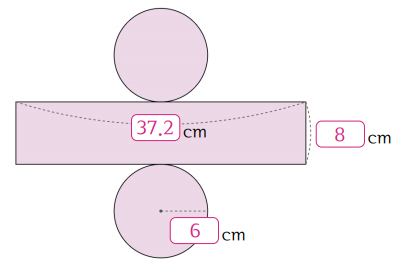
[참고] 원기둥의 전개도에는 합동인 원 두 개가 필요합니다. 원기둥은 위아래가 막혀있는 입체이므로 밑면인 원이 2개 필요합니다.
[참고] 옆면 직사각형의 가로 길이는 원의 지름이 아닌 원의 둘레(원주)입니다.
때에 따라 전개도를 90도 돌려서 주는 경우도 있습니다. 전개도를 접어서 원기둥이 되는 것은 변하지 않으므로 아래와 같은 경우도 원기둥의 전개도로 생각할 수 있습니다.
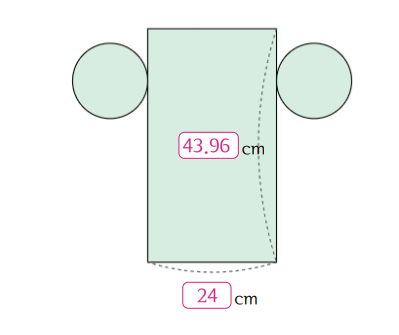
나아가 원기둥의 옆면은 직사각형이므로 가로와 세로를 곱하면 직사각형의 넓이를 계산할 수 있습니다.
[문제] 다음 원기둥의 전개도가 아래와 같을 때, 옆면의 넓이를 구하세요. (원주율: 3.14)
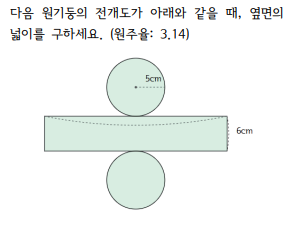
| [풀이] 옆면의 가로의 길이는 5×2×3.14=31.4cm 세로의 길이는 6cm입니다. 따라서 옆면의 넓이는 31.4×6=188.4$cm^2$입니다. |
답글 남기기