들어가며
안녕하세요? 셈나는교실입니다. 초등학교 4학년 1학기 수학 2단원 ‘각도’에서 가장 중요한 개념 중 하나는 바로 삼각형의 세 각에 관한 성질입니다.
모양과 크기가 제각각인 수많은 삼각형 속에는 변하지 않는 수학적 약속이 하나 숨어 있습니다.
이번 시간에는 삼각형의 세 각을 모두 더하면 항상 같은 값이 되는지, 그리고 이 성질을 이용해 모르는 각의 크기를 어떻게 구하는지 자세히 알아보겠습니다.
삼각형 세 각의 합
Q. 삼각형의 세 각을 모두 더하면 항상 $180^\circ$인 이유는 무엇인가요?
A: 삼각형의 세 꼭짓점을 잘라서 한 점에 모아보면 평평한 직선($180^\circ$)을 이루는 것을 확인할 수 있습니다.

위와 같은 삼각형의 세 각을 잘라서 한 곳에 모아볼까요?

위와 같이 각을 잘라내고 한 곳으로 모으면,

180도가 됨을 알 수 있습니다. (가운데 ㄴ처럼 보이는 각은 ㄱ을 180도 돌려서 ㄴ처럼 보이는 것임)
Q. 두 각의 크기만 알 때, 나머지 한 각은 어떻게 계산하나요?
A: 삼각형 세 각의 합이 $180^\circ$라는 성질을 이용하면 됩니다. 먼저 알고 있는 두 각의 합을 구한 뒤, 전체인 $180^\circ$에서 그 합을 빼주면 나머지 한 각의 크기를 마법처럼 찾아낼 수 있습니다. 공식으로 나타내면 다음과 같습니다.
$\text{모르는 각} = 180^\circ – (\text{알고 있는 두 각의 합})$
실전 예제 풀이
학습지에 수록된 문제들을 바탕으로 실제 계산 과정을 단계별로 정리했습니다. 각 상자 안의 풀이 과정을 꼼꼼히 확인해 보세요.
문제 1: 한 각이 $90^\circ$이고 다른 한 각이 $20^\circ$인 직각삼각형에서 나머지 한 각의 크기를 구하세요.
풀이:
1) 알고 있는 두 각의 합: $90^\circ + 20^\circ = 110^\circ$
2) 전체 합에서 빼기: $180^\circ – 110^\circ = 70^\circ$
정답: $70^\circ$
문제 2: 두 각의 크기가 각각 $55^\circ$, $75^\circ$인 삼각형의 빈칸에 알맞은 수를 써넣으세요.
풀이:
1) 두 각의 합 계산: $55^\circ + 75^\circ = 130^\circ$
2) 나머지 각 찾기: $180^\circ – 130^\circ = 50^\circ$
정답: $50^\circ$
문제 3: 한 각이 $120^\circ$인 둔각삼각형에서 다른 한 각이 $30^\circ$일 때, 마지막 각의 크기를 읽어보세요.
풀이:
1) 두 각의 합 계산: $120^\circ + 30^\circ = 150^\circ$
2) 나머지 각 찾기: $180^\circ – 150^\circ = 30^\circ$ (이 삼각형은 두 각이 같은 이등변삼각형이기도 합니다.)
정답: $30^\circ$
학습지 살펴보기
아래 자료를 통해 전체 15문항이 수록된 학습지를 공부할 수 있습니다. 직접 각도기를 들고 재어보며 수학의 즐거움을 느껴보세요.
초4-1-각도-삼각형-세-각의-크기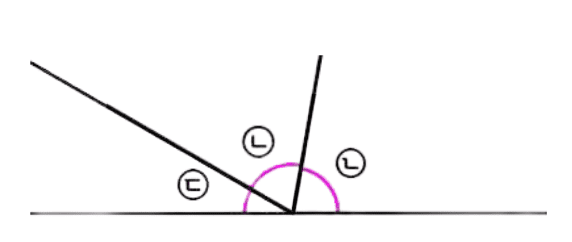
답글 남기기